太原 郭大焱
十二个正五边形组成一个十二面球体。在球体表面上共有二十个顶点,用 1~10、12~21 共二十个数填在顶点上,使每个五边形角上五个数之和均为 55。见图A和图B,它们都是球体的展开图。
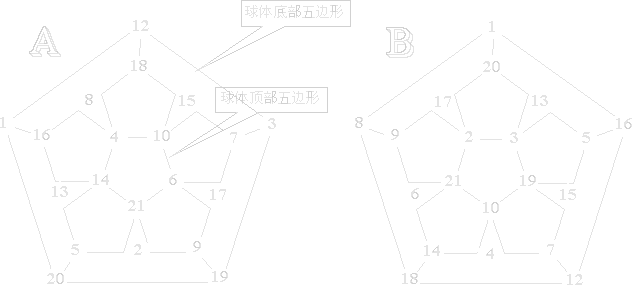 | |
 |
图A和图B为非连续数填数,图C则用 1~20 填数后,再用 21~32 十二个数填在五边形中间,最后使五边形角上五个数和中间数相加六数之和均相等,为 79。
当然也可用 1~12 填在五边形中间,13~32 填在二十个接点上,这样一来,每个五边形六数之和就都等于 119 了。 图D为图C的补数形式,(接点数为 21 减原数,中间数为 53 减原数)结果不变。 |
备注: