一组有特色的幻方
太原 郭大焱
返回索引 | 上一页 | 下一页
四、可拆幻方(七阶~十阶)
同样, 特优完美幻方也可拆,详见下面所示。
第一型(全对称图案)
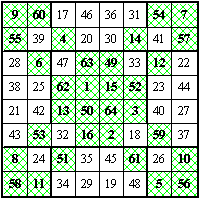 |
第二型(角对称图案)
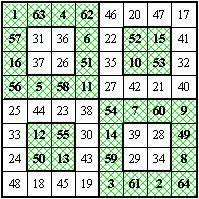 |
第三型(半对称图案)
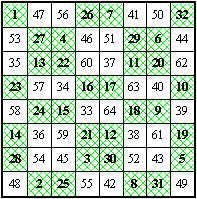 |
前两型两个幻方均为一般可拆幻方,1~64 数字排列为全对称,两个八阶四数幻方,其幻和均为 130 。幻方可分成相等的四部分,左右、上下互换,结果不变。此类幻方还有多种图案的设计和数字的排列。
最后第三型这个幻方却是个特优完美可拆幻方,幻和为 260 ,两条对角线各数平方和为 11 260 ,立方和为 548 600 。若把幻方左右对分易位,则两条对角线各数平方和为 11 100 ,立方和为 53 300 (7 、29 、20 、10 、58 、36 、45 、55 和 26 、4 、13 、23 、39 、61 、52 、42 )。若把幻方 1 、3 、5 、7 列(行)和 2 、4 、6 、8 列(行)互换位置,结果幻方性质不变,见图 4-1,但两条对角线各数平方和变为 11 228 ,立方和 545 480。若把幻方左右对分易位,则两条对角线各数平方和为 11 132 ,立方和为 536 120 (41 、51 、62 、40 、24 、14 、3 、25 和 56 、46 、35 、57 、9 、19 、30 、8 )。两个八阶四数幻方分别由 1~32 和 33~64 各三十二个数字组成,见图 4-2 和图 4-3 。
上一页 | TOP | 下一页 | 返回索引





