一组有特色的幻方
太原 郭大焱
返回索引 | 上一页 | 下一页
四、可拆幻方(七阶~十阶)
图 4-2 还有很多变化,如幻方四大格左右各大格对称旋转同一角度、上半部两大格互换位置、或只是第一行和第四行或第二行和第三行四个数互换位置(如 1 、26 、23 、16 和 7 、32 、17 、10 或 27 、4 、13 、22 和 29 、6 、11 、20 )结果,幻方性质都不变,此时若图 4-3 也作相应的变化,那么图 4-2 和图 4-3 合起来,仍然是一个八阶特优可拆完美幻方。
这是一个非常有趣的全对称九阶可拆幻方,由 1~81 顺序数组成,见右下图。它有以下特点:
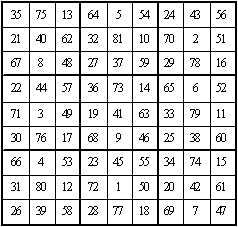
一、它虽然不是完美幻方,但是它的幻和数比完美幻方多得多,我们把它划分成相等的九部分(九大格)每部分九个数之和均等于 369,每大格的同一相应位置上九数之和也是 369,(如每大格左上角的九个数字 35 、64 、24 、22 、36 、65 、66 、23 、34)。每大格行和列三数之和均为 123(共 54 组),此外还有四条对角线上三数之和也为 123,这样任意取三组,九数之和都是 369 的组合就有十几万种了。
二、它还是一个九阶双向可拆幻方,可拆成横向的三个九阶三数幻方,见图 4-4 ~ 图 4-6;同时可拆成纵向的三个九阶三数幻方见图 4-7 ~ 图 4-9, 粗黑字为对角线上的数字,幻和均为 123 。
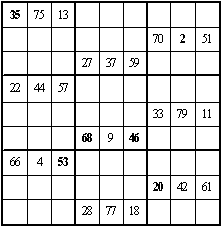
图 4-4 |
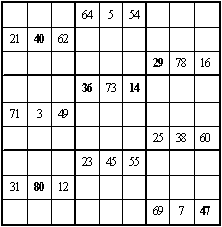
图 4-5 |
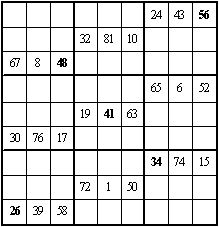
图 4-6 |
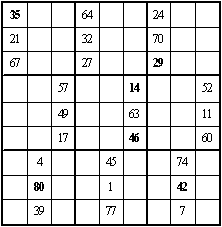
图 4-7 |
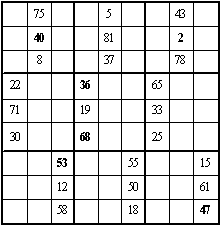
图 4-8 |
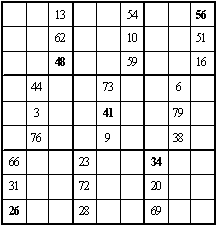
图 4-9 |
上一页 | TOP | 下一页 | 返回索引












